ANALYSIS >> Tangenten-Steigung

Von der Sekanten- zur Tangenten-Steigung

Differenzenquotient und Differentialquotient

(für Interessierte ab ca. 11./E Jg.)

Die Herleitung der Ableitungsformel ist ein umfangreiches Kapitel. Im Schulunterricht werden Sie sich vermutlich etliche Stunden damit beschäftigen. Hier kann dieser Prozess nicht ersetzt, aber zum Nachdenken über einzelne Teilaspekte angeregt werden.

"Brauchen wir das in der Arbeit???" stellen Sie jetzt vielleicht die typische SchülerInnen-Frage. Meine Antwort: Die meisten Details vermutlich nicht! (Wie Sie vielleicht auch schon gesehen haben, hier auf der Seite wird es kein "Kompakt-Training" geben, keine Rechenschritte, die Sie unbedingt "einpauken" sollten.) Das bedeutet jetzt aber nicht, dass Sie sich zurücklehnen und gar nichts machen sollen. Versuchen Sie bei der Einführung eines so komplexen Themas, möglichst viele der Grundgedanken wenigstens im Ansatz zu erfassen (ohne gleich Angst zu bekommen, dass mathematische Erfindungen, für die die Menschheit Jahrhunderte brauchte(!), von Ihnen in der nächsten Arbeit erwartet werden). Wenn Ihnen dabei gelingt, den gedanklichen "Roten Faden" zu erkennen, dann wird Ihnen im Folgenden insgesamt vieles leichter fallen. Sowohl im Mathematik-Unterricht als auch bei eventuellen Verständnisfragen in der nächsten Arbeit.

(Die Formeln, die Sie für Analysis Routine-Aufgaben später dauernd brauchen werden, finden Sie auf der nächsten Seite, siehe Ableiten).

Viel Erfolg!

✩ Einleitende Fragestellung ✩

Für eine sichere Spielplatz-Rutsche müssen u.a. folgende zwei Bedingungen gelten:

(1) »Der Neigungswinkel des Rutschteils zur Horizontalen darf durchschnittlich 40° nicht überschreiten.«

(2) »Winkel über 60° sind unzulässig«

(s. sichere-kita.de )

Der Verlauf der hier abgebildeten Rutsche soll im Bereich für -0,6 ⩽ x ⩽ 1 durch folgende ganzrationale Funktion modelliert werden

f (x) = \frac{19}{40} x^{4} - \frac{11}{20} x^{2} - \frac{4}{5} x + \frac{7}{8}

Durchschnittliche Steigung

Sekanten-Steigung

Um den durchnittlichen Neigungswinkel α zu ermitteln, berechnet man zuerst die Steigung m_PQ der Sekante durch die Punkte P(-0,6|f(-0,6)) und Q(1|f(1)) mittels des Differenzenquotienten:

m_{P Q} = \frac{y_{Q} - y_{P}}{x_{Q} - x_{P}} = \frac{f (x_{Q}) - f (x_{P})}{x_{Q} - x_{P}}

Bezeichnung "Differenzenquotient" bitte merken!

Erklärung ganz einfach: Der Bruch "Zähler durch Nenner" insgesamt ist ein Quotient. Über und unter dem Bruchstrich wird jeweils "Minus gerechnet", d.h. je eine Differenz gebildet. Daher: "Differenzen-Quotient"

Graph von f mit Sekante PQ. Durchschnittliche Steigung m_PQ

Sie erkennen die Formel wieder? (Siehe Steigungs-Dreiecks-Formel zum Berechnen von Geraden-Steigungen). Damit kann man weiter rechnen:

m_{P Q} = \frac{y_{Q} - y_{P}}{x_{Q} - x_{P}} = \frac{f (1) - f (- 0, 6)}{1 - (- 0, 6)}

m_{P Q} \approx \frac{0 - 1, 21856}{1, 6} \approx 0, 7616

\tan (α) \approx - 0, 7616

\Rightarrow

α \approx - 37, 29 °

Somit wurde gezeigt, der Betrag des durchnittlichen Neigungswinkels α ist hier kleiner als 40°.

Bedingung (1) für die Rutsche ist erfüllt!

Steigung einer Kurve in einem Punkt

Gesucht: "Tangenten"-Steigung

Die große Frage ist, wie kann man herausfinden, ob auch Bedingung (2) erfüllt wird?

(a) Das Besondere einer Wellenrutsche ist ja, dass sie - zum großen Vergnügen der rutschenden Kinder - an verschiedenen Stellen ganz unterschiedlich steil ist! Das bedeutet: Man muss in verschiedenen Punkten untersuchen, wie steil die Kurve jeweils ist.

(b) Wir kennen bisher nur Steigungen von Geraden. Was versteht man nun unter der "Steigung einer Kurve in einem Punkt"?

Vorläufig formuliert: Man meint die Steigung einer Geraden, die die Kurve genau in diesem Punkt berührt (eine "Tangente") (siehe Bild-Animation).

(c) Vorschau: Auch dann, wenn man in jedem Punkt der Kurve deren Steigung bestimmt kann, wird noch die Frage bleiben: Wie findet man den Punkt, in dem die Rutsche am steilsten ist? Um dann letztendlich zu klären, ob auch der steilste Winkel unter 60° liegt und damit Bedingung (2) erfüllt wäre. (Näheres dazu siehe Analysis / Kurvendiskussion.)

Gesucht: "Tangenten" (Berühr-Geraden) in verschiedenen Pukten der Kurve.

Mehr zu den Begriffen "Sekante" und "Tangente" (klick auf Dreieck)

Aus der Mittelstufe ist der Begriff "Tangente an einen Kreis" bekannt. Dieser lässt sich aber NICHT so einfach auf eine allgemeine Kurve übertragen.

✩ Ziel ✩

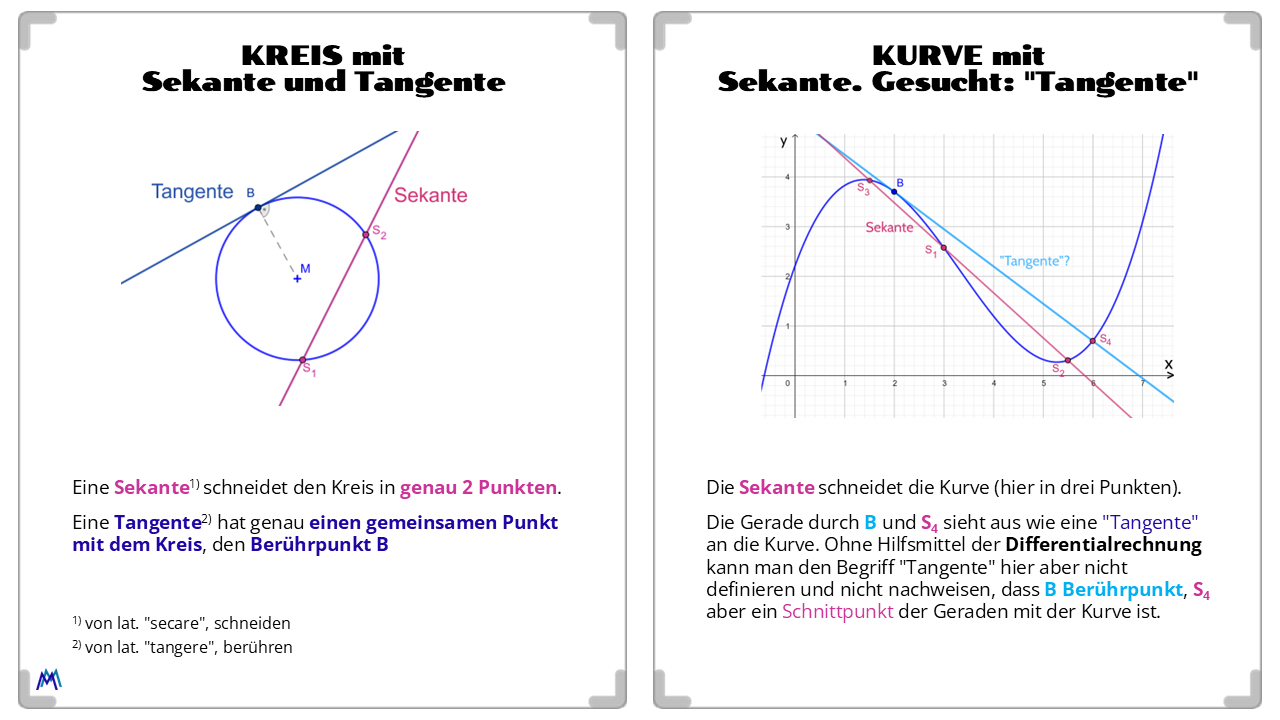
Gesucht wird ein VERFAHREN, wie man zu einer gegebenen Funktion f für jeden Punkt ihres Graphen DIE STEIGUNG DER KURVE IN DIESEM PUNKT ermitteln kann - sofern diese überhaupt eindeutig bestimmbar ist.

Spätestens beim letzten Teil obigen Satzes denken Sie wohl "typisch Mathematiker, müssen die immer alles so kompliziert ausdrücken?"

Ja! man muss. Auch die genannte Einschränkung muss man aussprechen, wie das folgende Beispiel zeigt.

Exkurs: Nicht jede Funktion ist differenzierbar!

Nicht bei jeder Funktion lässt sich in jedem Punkt eine eindeutige(!) Steigung definieren.

Betrachten Sie einmal folgenden Entwurf zum Querschnitt einer (fiktiven) Rutsche (s. Bild).

In Punkt Z ist diese nicht unfallsicher. Zunächst würden die Kinder sehr flach bis fast waagrecht ruschten, dann, nach Punkt Z geht es plötzlich ziemlich steil abwärts. Direkt bei Z, beim "Knick" der Kurve, sind eine harte Kante, eventuell zerrissene Hosen und "Aua"-Rufe zu befürchten.

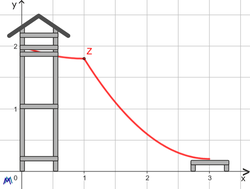
Mathematisch formuliert: Die Kurve hat in Punkt Z keine eindeutige Steigung (sie kann ja nicht gleichzeitig flach und steil sein!).

Man sagt: In Punkt Z ist die zugrunde liegende Funktion nicht differenzierbar.

✩ Zeichnerische Annäherung ✩

Als "Graphisches Differenzieren" bezeichnet man das Bestimmen von Steigungen einer Kurve in verschiedenen Punkten nach Augenmaß. Übungen dazu (auch Aufgabentypen wie sie gerne in Klausuren vorkommen!) finden Sie in Ihrem Schulbuch od. geeigneten Erklär-Videos. (Unterseite zu diesem Tema hier in Planung.)

✩ Grundidee für das rechnerische Verfahren ✩

Bildquelle: MM-Mathe. Zeichnung LWY

Wie häufig in der Mathematik (und im Leben?) geht man hier erst einmal von Bekanntem aus um Neues darauf aufzubauen.

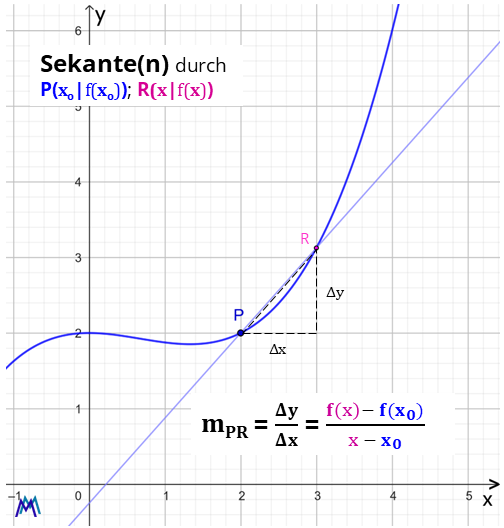
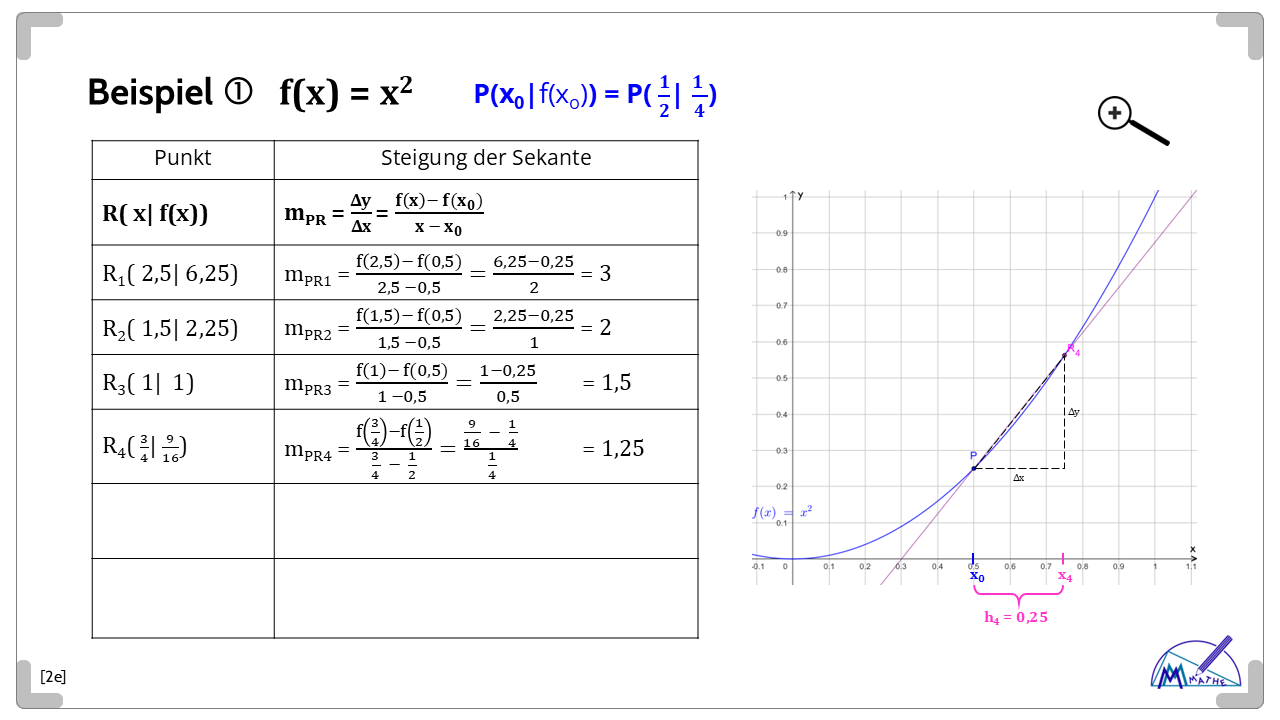
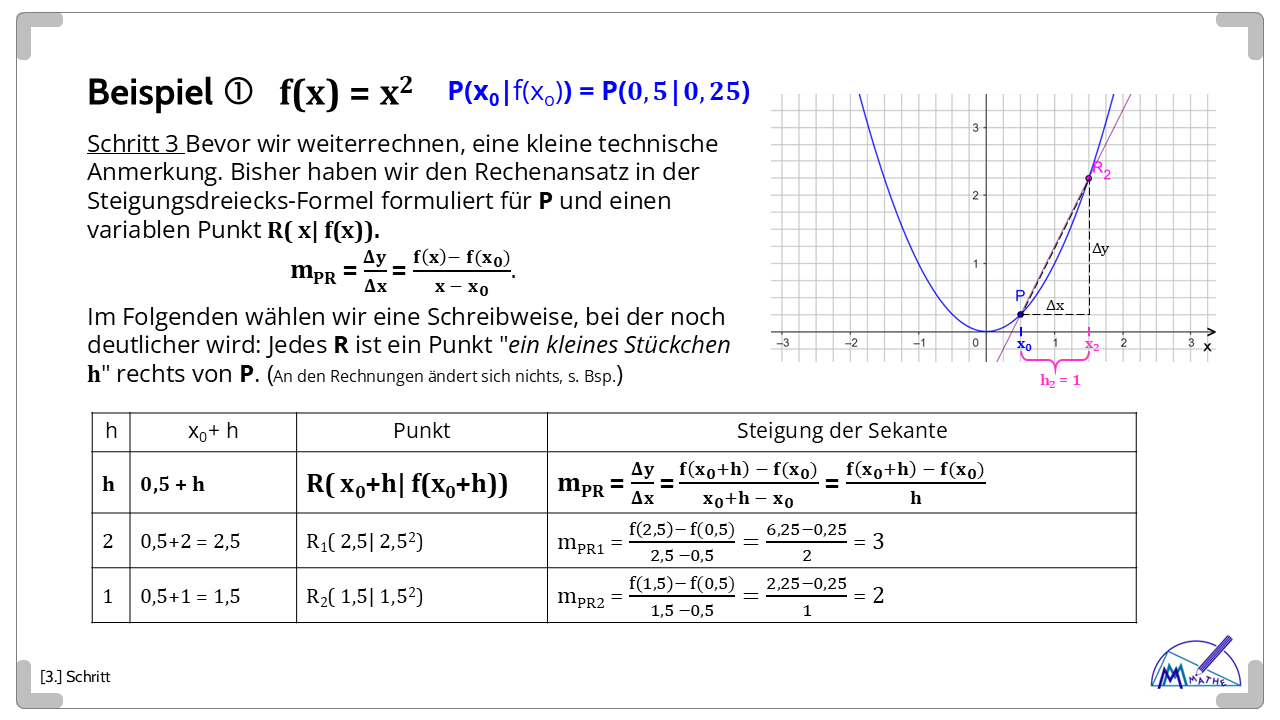
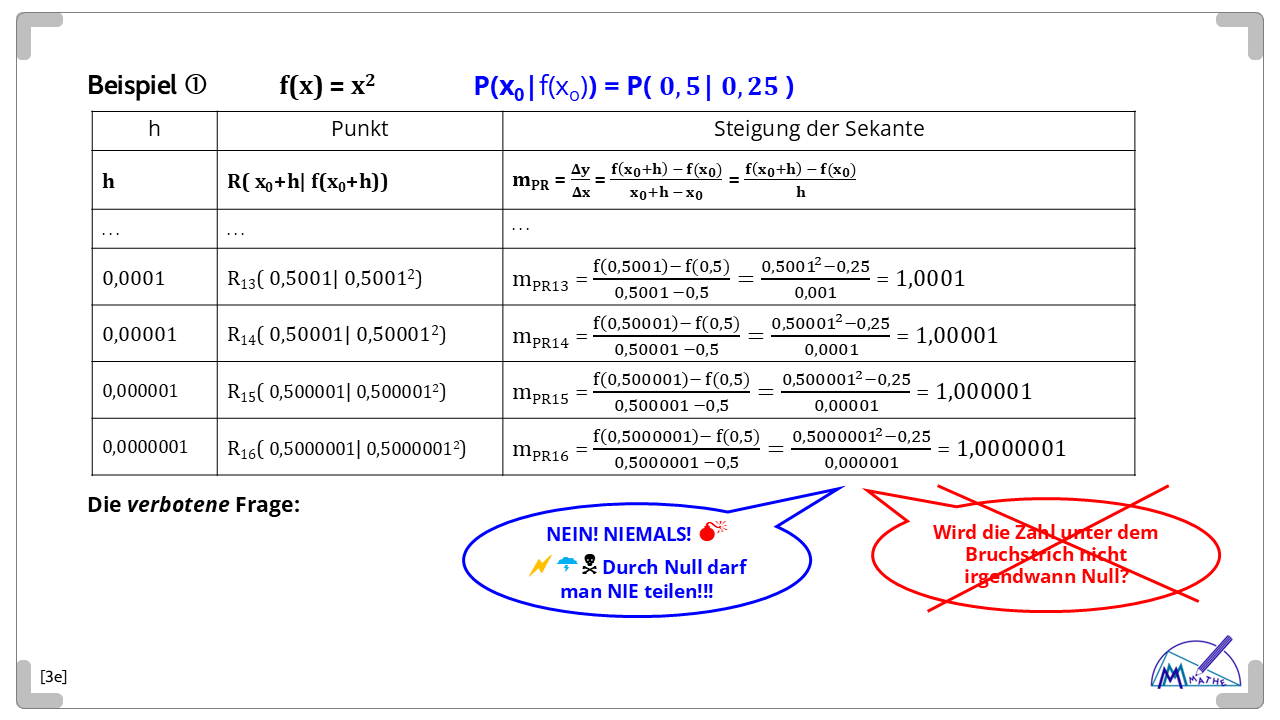
Hier bedeutet das: Es ist bekannt, wie man zu einer gegebenen Funktion f die Steigung einer Sekanten durch zwei Punkte P und R ihres Graphen mit Hilfe des Differenzenquotienten berechnet.

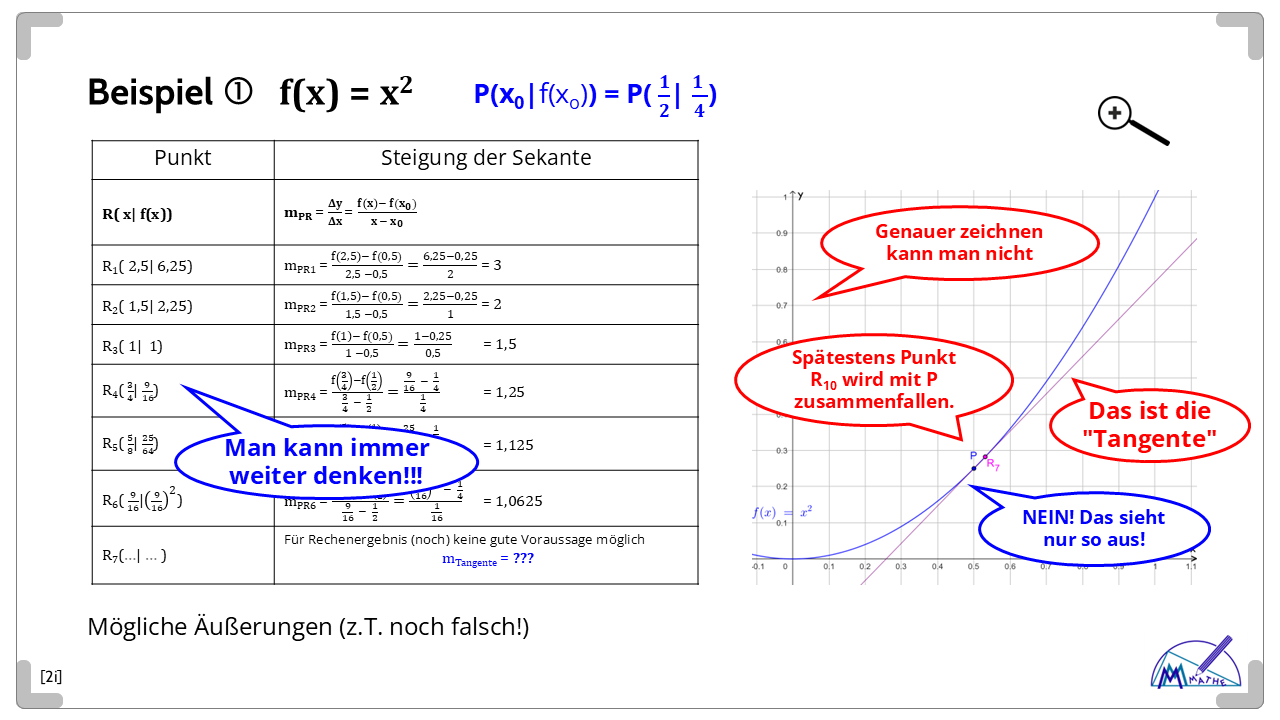
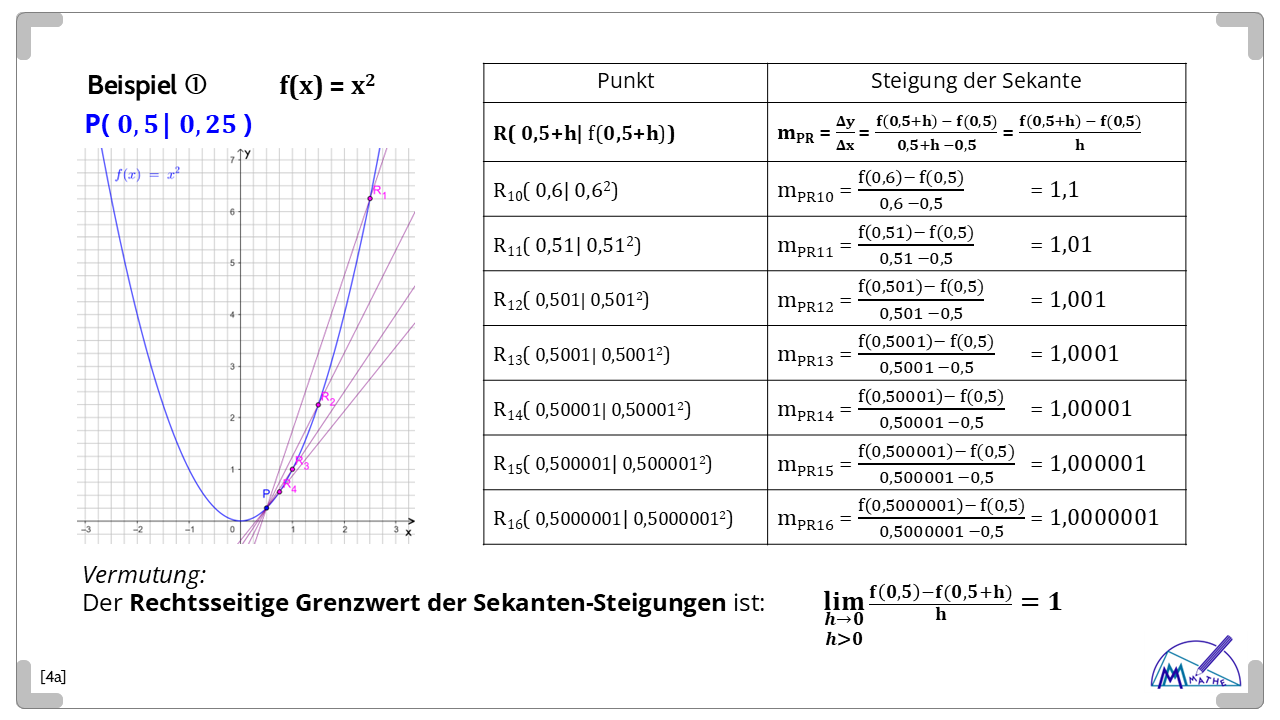
Die neue Idee ist: Um sich der gesuchten "Berühr-Geraden" ("Tangente") anzunähern lässt man nun Punkt R immer näher zu P wandern.

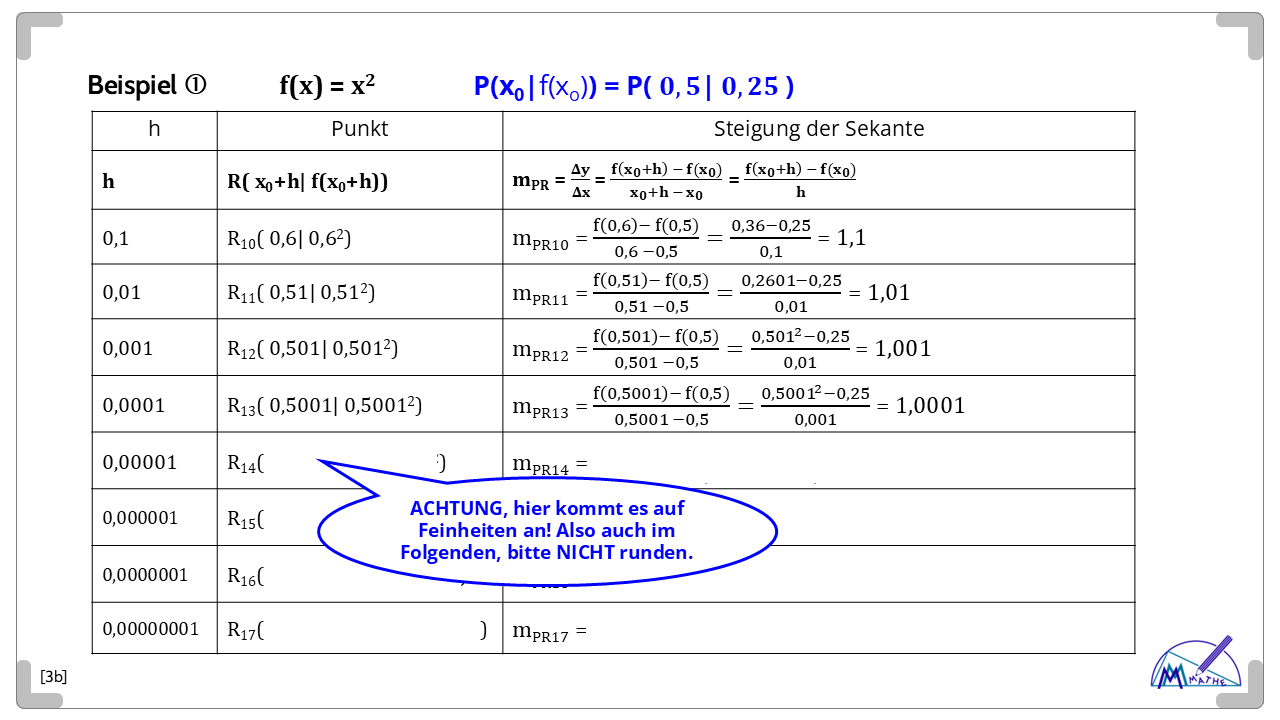
Die Frage ist dann: Gibt es einen Grenzwert der Sekanten-Steigungen, den sog. Differentialquotienten

$\lim_{x \to x_{o}} \frac{f (x) - f (x_{0})}{x - x_{0}}$ ?

Falls ja, kann man damit die bisher nur vage umschriebenen Begriffe endlich klar definieren: Diesen Grenzwert wird man Steigung der Kurve in Punkt P nennen, zukünftige Abkürzung: f'(x₀).

Als Tangente an den Graphen von f in Punkt P wird man eine Gerade bezeichnen, die durch Punkt P geht und genau dieses f'(x₀) als Steigung hat.

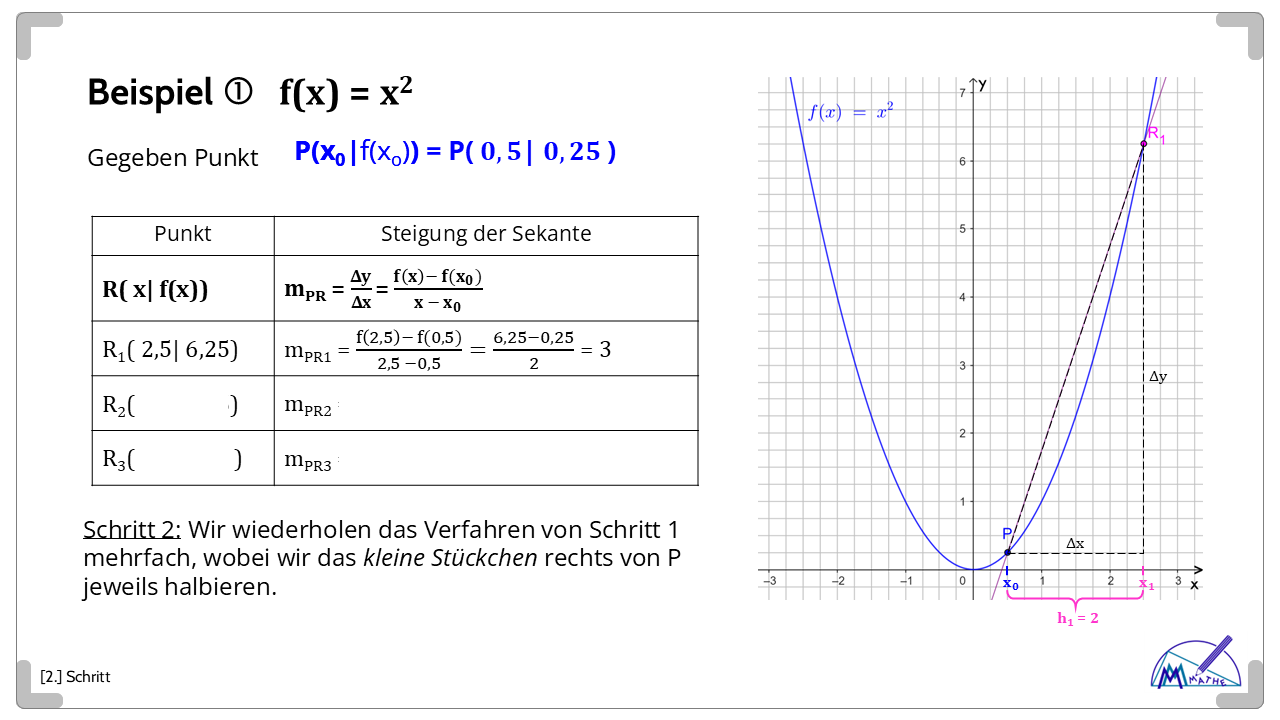
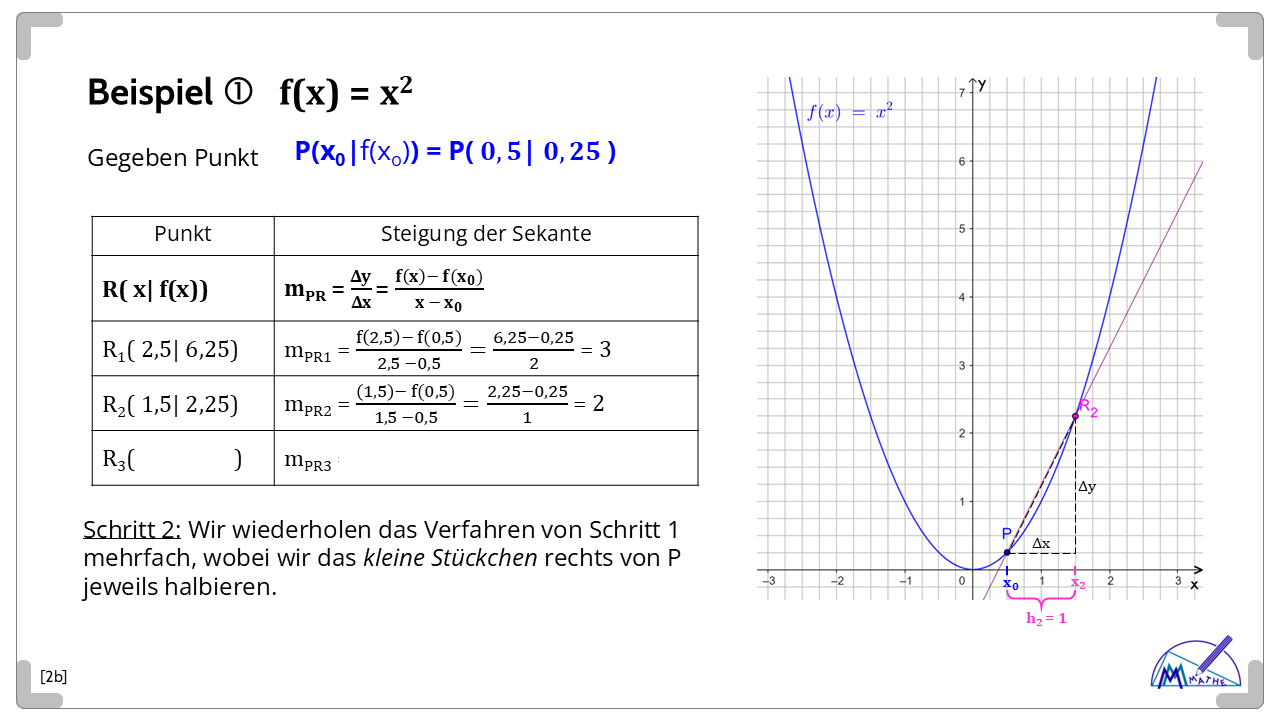
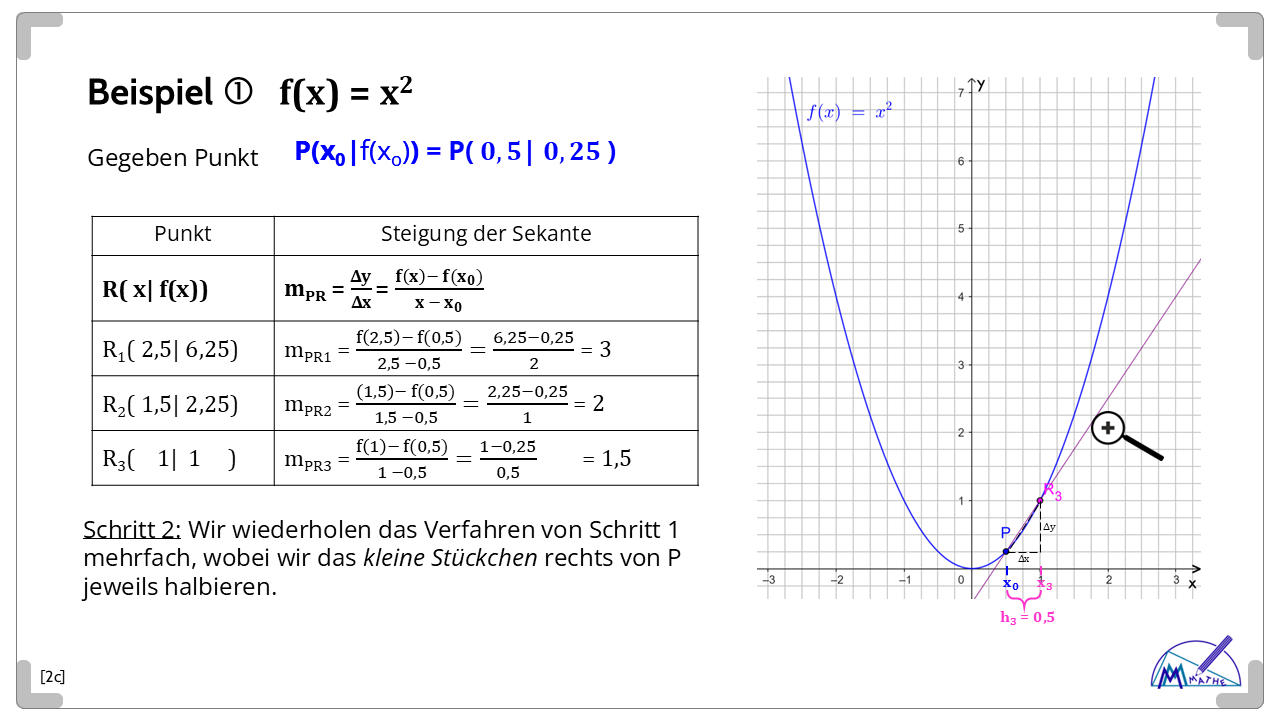
Berechnung der Tangenten-Steigung

✩ Herleitung der Formel für die ERSTE Beispiel-Funktion ✩

Bilderserie als Selbstlern-Kurs (zu Quellen, Ergänzungen, klick auf Dreieck)

Bildquellen, Details:

[3c] Portrait Gottfried Wilhelm Leibniz 1700

Painting by Johann Friedrich Wentzel, 1700

Public Domain, https://commons.wikimedia.org/w/index.php?curid=6886474

[3c] Portrait Sir Isaac Newton 1689

https://commons.wikimedia.org/w/index.php?curid=101534333

[4] Limes-Denkmal in Gundelshalm

https://commons.wikimedia.org/wiki/File:Limes-Denkmal_in_Gundelshalm2.JPG

Sonst alle INFO-Bilder: MM-Mathe

---

Informationen zum Thema Limes:

https://de.pons.com/%C3%BCbersetzung-2/latein-deutsch/limes

https://de.wikipedia.org/wiki/Limes_(R%C3%B6misches_Reich)

---

Fortsetzung der Bilderserie noch im Aufbau (bitte etwas Geduld)

(Notizen MM

Bis Abl. zu f(x) = x^2

Dann Info 0 ?

Exkurs 2 nicht jede ... differenzierbar

Info: Alle ganzrat. , Trig ...

werden nichtlange alle hier beweisen,

Aber wenigstens alle Pot-Fkt ...)

Alternative Herleitungen: (am besten hier am Schluss)

Wir haben angeregt durch unser Einführungsbeispiel

gesehen, wie man über Grenzwert-Bildung von "Durchschnittlichen Steigungen" zur: "Steigung einer Kurve in einem.Punkt" gelangt.

Ensprechnde Überlegungen führen bei Zeit-Weg Funktionen von der "Durchschnittlicher Geschwindigkeit" zur "Momentanen Geschwindigkeit (zu einem Zeitpunkt)".

Oder noch allgemeiner von der "Durchschnittlichen Änderungsrate" einer Funktion zur "lokalen" bzw. "momentanen Änderungsrate"

Lernpfad ZUM.de

matheskills2go (verwendet "h-Mehode"

Hinweis Physik / Newton

Video MathemaTrick (evtl. schon bei f_3(x) = x^3)

Playlist zu diesem Thema z.B. von Daniel Jung enthält 47 Videos.