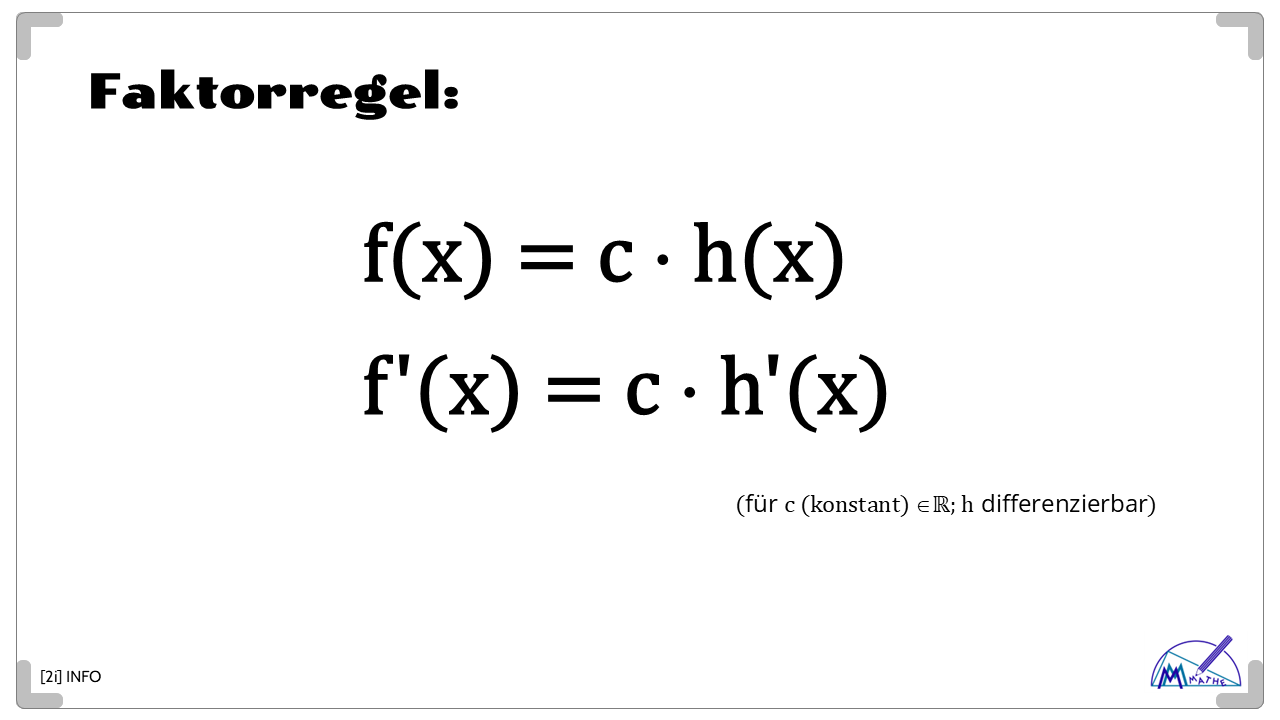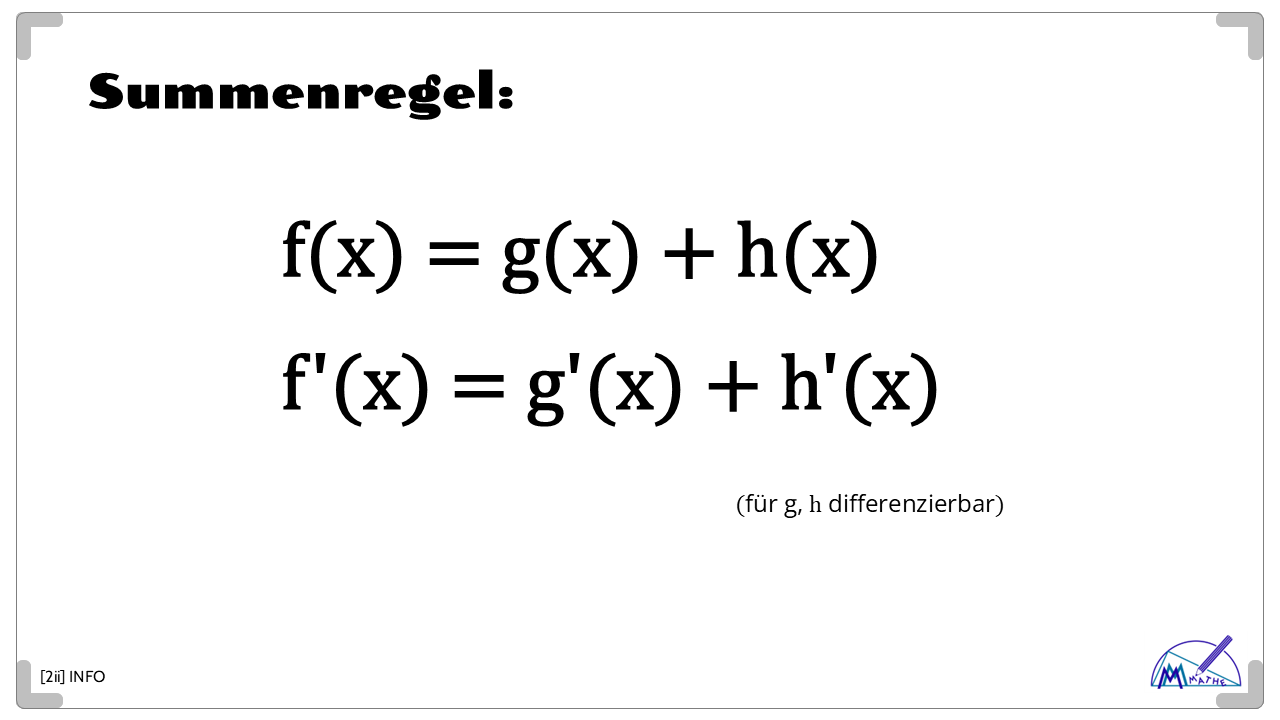ANALYSIS >> Ableiten
Ableiten (1)
Potenzfunktionen und Ganzrat. Fkt.
11. / 12. Jg. (E Jg. / Q1)
Seite im Aufbau (bitte etwas Geduld)
Informationen:
✦ KOMPAKT TRAINING (WIEDERHOLEN UND ÜBEN) ✦
✧ SCHRITT FÜR SCHRITT ✧ ERKLÄRUNGEN von Anfang an.
Mehr siehe Ableiten II
Erste Ableitungsregeln
[A] Ableiten von Potenzfunktionen
Die Herleitung dieser Formel war ja sehr aufwändig (siehe ...).
Jetzt dürfen wir sie anwenden. Das geht zum Glück so einfach, gleich mit ein paar kleinen Übungen direkt hier auf der Seite. (Klick auf Dreieck zum Anzeigen der Lösungen und Begründungen).
| Funktion | 1.Ableitung |
|---|---|
|
f(x) = xn für n ∈ N |
f'(x) = n∙xn-1
|
| f(x) = x5 | f'(x) = 5x4 |
|
Leite ab: 📝 f(x) = x4 f(x) = x2 f(x) = x3 f(x) = x8 |
f'(x) = ?f'(x) = 4x3 f'(x) = 2x = 2x1 f'(x) = 3x2 f'(x) = 8x7 |
Sonderfall:
| Funktion | 1.Ableitung |
|---|---|
|
Leite ab: f(x) = x |
f'(x) = ?f'(x) = 1 |
Begründung:
|
f(x) = x = x1
|
f'(x) = 1x1-1 = 1x0 f'(x) = 1 |
|
Zur Erinnerung x0 = 1 Mehr siehe ➔ POTENZEN II Schritt F |
|
[B] Ableiten von Ganzrationalen Funktionen
Faktorregel
Die einfache Faktorregel gilt für jede differenzierbare Funktion (siehe oben: INFO[2]). Also auch für jede Potenzfunktion, die mit einer konstanten Zahl (die nichts mit der Variablen x zu tun hat) multipliziert wird.
Beim Ableiten gilt dann:
| Funktion | 1.Ableitung |
|---|---|
|
f(x) = a∙xn für a ∈ R und n ∈ N |
f'(x) = a∙n∙xn-1
|
| f(x) = 4x3 | f'(x) = 12x2 |
|
Leite ab: 📝 f(x) = 2x5 f(x) = 100x4 f(x) = 4x2 f(x) = 5 f(x) = 6x
|
f'(x) = ?f'(x) = 10x4 f'(x) = 400x3 f'(x) = 8x f'(x) = 0 +) f'(x) = 6 +) +) siehe Sonderfälle |
Sonderfall:
| Funktion | 1.Ableitung |
|---|---|
|
f(x) = c c ∈ R konstant |
f'(x) = ?f'(x) = 0 |
Begründung:
|
f(x) = c ∙ 1 = c ∙ x0
|
f'(x) = 0 ∙ c ∙ x0-1 f'(x) = 0 |
|
Zur Erinnerung x0 = 1 Mehr siehe ➔ POTENZEN II Schritt F |
|
Summenregel
Jetzt wird es noch praktischer. Allgemein gilt die "Summenregel":
Funktion
f(x) = g(x) + h(x)
für g, h differenzierbar
1.Ableitung
f'(x) = g'(x) + h'(x)
Diese gilt auch für jede Summe von Potenzfunktionen und deren Vielfachen, d.h. für ALLE Ganzrationalen Funktionen!
Bsp. allgemeine ganzrat. Fkt. 5.Grades:
Funktion
f(x) = ax5 + bx4+ cx3+ dx2 + ex + f
1.Ableitung
f'(x) = 5ax4 + 4bx3+ 3cx2+ 2dx + e
Weitere Beispiele:
Funktion
a) f1(x) = x5 + 3x4 + 2x3 + 0,5x2 - 10x + 8
Leite ab: 📝
b) f2(x) = 2x4 + x3 - 5x2 + 3x - 17
c) f3(x) = 7x8 - 3x6 + 113
1.Ableitung
a) f1'(x) = 5x4 + 12x3 + 6x2 +1x - 10
?
b) f2'(x) = 8x3 + 3x2 - 10x + 3
c) f3'(x) = 56x7 - 18x5
Mehr siehe ➔ KOMPAKT-TRAINING